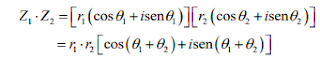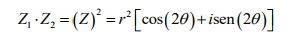UNIDAD I NUMEROS COMPLEJOS

Los números complejos nos ayuda a dar un sentido a las cantidades cuya raíz se aplique a un numero negativo y así poder dar solución a operaciones en torno a los números reales.

Resultan de gran importancia debido a su aplicación en diversas áreas como la electricidad, hidráulica, aerodinámica, matemáticas entre otras, lo que la hace indispensable en todas las ramas de la Ingeniería:"En el estudio d e un fenómeno físico o químico necesitamos hacer uso de las ecuaciones diferenciales, ordinarias y parciales; para resolver dichas ecuaciones se utilizan a los números complejos por lo general; por ejemplo para resolver un problema de ondas se utiliza el  método de variables separables donde se aplica la serie de Fourier."

En esta unidad se discutirá y analizará el origen y definición de los números complejos así como la realización de operaciones fundamentales. Se estudiará el valor absoluto de un número complejo, las formas polar y exponenciales de estos números así como el Teorema de Demoivre y consecutivamente se estudiarán las ecuaciones polinómicas.

Dichos temas nos servirán como herramienta básica para el posterior estudio de las ecuaciones diferenciales; en el área de electrónica nos será indispensable para estudio de los circuitos eléctricos, oscilaciones, vibraciones y fenómenos ondulatorios.

Infografía de la unidad

Competencias específicas:
Utiliza los números complejos, sus representaciones y las operaciones entre ellos para tener una base de conocimiento a utilizar en ecuaciones diferenciales y en diferentes aplicaciones de ingeniería.

Competencias genéricas: 
Capacidad de abstracción, análisis y síntesis. Capacidad para identificar, plantear y resolver problemas. Capacidad de aprender y actualizarse permanentemente. Capacidad de trabajo en equipo.



Bibliografía:

IAkovlev, G. (1984). Álgebra y principios de análisis. Moscú: Mir.
Queysanne, M. (1990). Algebra básica. Barcelona: Vicens-Vives.

1.1 Definición y origen de los números complejos.

La primera referencia conocida a raíces cuadradas de números negativos proviene del trabajo de los matemáticos griegos, como Herón de Alejandría en el siglo I antes de Cristo, como resultado de una imposible sección de una pirámide. Los complejos se hicieron más patentes en el Siglo XVI, cuando la búsqueda de fórmulas que dieran las raíces exactas de los polinomios de grados 2 y 3 fueron encontradas por matemáticos italianos como Tartaglia, Cardano.

Aunque sólo estaban interesados en las raíces reales de este tipo de ecuaciones, se encontraban con la necesidad de lidiar con raíces de números negativos. El término imaginario para estas cantidades fue acuñado por Descartes en el Siglo XVII y está en desuso. La existencia de números complejos no fue completamente aceptada hasta la más abajo mencionada interpretación geométrica que fue descrita por Wessel en 1799, redescubierta algunos años después y popularizada por Gauss. La implementación más formal, con pares de números reales fue dada en el Siglo XIX.

Los números complejos, se expresan a través de la suma de un número real y un número imaginario. Al entero real se le denomina parte real del número complejo y al número imaginario se le llama parte imaginaria del número complejo. Una de las muchas formas de expresar a los números complejos sería:

 z = a + bi

Los números complejos existen para cubrir un aspecto que los números reales no son capaces de solventar. Por ejemplo, a través de los números reales no podemos expresar las raíces pares de un número negativo, por ejemplo:

Fue entonces que Leonhard Euler en 1777 introdujo el concepto de numero imaginario al asignar la raíz de un número negativo: 

De esta manera, los números imaginarios son capaces de expresar todas las raíces de un polinomio, raíces reales y raíces imaginarias. 

1.2 Operaciones fundamentales con números complejos.

Suma

Primero, considera la siguiente expresión.

(6x + 8) + (4x + 2)

Para simplificar esta expresión, combina los términos semejantes, 6x y 4x. Estos son los términos semejantes porque tienen la misma variable con el mismo exponente. De manera similar, 8 y 2 son términos semejantes porque ambos son constantes, sin variables.

(6x + 8) + (4x + 2) = 10x + 10

De la misma manera, puedes simplificar expresiones con radicales.

Puedes sumar  con  porque ambos términos tienen el mismo radical, , del mismo modo que 6x y 4x tienen la misma variable y exponente.

El número i parece una variable, pero recuerda que es igual a . Lo interesante es que no hay reglas nuevas de las cuales preocuparse, ya sea que lo trates como una variable o un radical, aplican las mismas reglas para sumar y restar números complejos. Combinas las partes imaginarias (los términos con i) y combinas las partes reales.

Por ejemplo:

Sumar. (−3 + 3i) + (7 – 2i)

−3 + 3i + 7 – 2i         Reacomoda las sumas para juntar los términos semejantes

−3 + 7 + 3i – 2i

−3 + 7 = 4 y                  Combina los términos semejantes

3i – 2i = (3 – 2)i = i

Respuesta: (−3 + 3i) + (7 – 2i) = 4 + i

Restar. (−3 + 3i) – (7 – 2i)

(−3 + 3i) – (7 – 2i) =     Asegúrate de distribuir el signo de resta a todos los términos del sustraendo.

−3 + 3i – 7 + 2i

−3 – 7 + 3i + 2i   Reacomoda las sumas para juntar los términos semejantes.

−3 – 7 = −10 y

3i + 2i = (3 + 2)i = 5i  Combina los términos semejantes.

Respuesta    (−3 + 3i) – (7 – 2i) = 10 + 5i

Multiplicación

De nuevo, considera la siguiente expresión. Antes de seguir leyendo, piensa en cómo la podrías simplificar.

(5x)(−3x)

Puedes simplificar multiplicando los coeficientes, luego las variables.

(5x)( −3x)	=	(5)( −3)(x)(x)
	=	−15x2

Multiplicar dos números imaginarios (¡pero no complejos!) funciona del mismo modo, pero hay un paso adicional. Empieza con el mismo método para multiplicar 5i y −3i.

(5i)( −3i)	=	(5)( −3)(i)(i)
	=	−15i2

Hasta ahora todo va bien, pero el i² se puede simplificar más.

Cuando multiplicas una raíz cuadrada por sí misma, obtienes el número dentro del radical. Esto es lo que significa una raíz cuadrada.

Bueno, i también es una raíz cuadrada. Es igual a .

Entonces, el último paso para simplificar (5i)( −3i) = −15i² es reemplazar i² con −1.

(5i)( −3i) = (5)( −3)(i)(i) = −15i2 = −15(−1) = 15

División

Hasta ahora, cada operación con números complejos ha funcionado de la misma manera que con expresiones radicales. Esto no debería sorprenderte, el número i es el radical, después de todo, ¡ por lo que los números complejos son expresiones radicales!

Veamos a la división en dos partes, como hicimos con la multiplicación. Primero, veamos la situación cuando el divisor es un monomio.

Simplifica. −24i ÷ 6

Respuesta

−24i ÷ 6 = −4i

Ejemplo

(56 – 8i) ÷ (14 + 10i)

Respuesta (56 – 8i) ÷ (14 + 10i) = 

1.3 Potencias de “i”, módulo o valor absoluto de un número complejo.

Sea z=(a +bi) un número complejo cualquiera. Llamaremos módulo del número complejo z, al número real dado por

y lo denotaremos por lzI. El módulo se interpreta como la distancia al origen del número z.

Ejemplo:

1.4 Forma polar y exponencial de un número complejo.

Hemos visto la representación rectangular de un número complejo y como se definen las operaciones elementales para un número complejo en forma rectangular. Sin embargo, existen otras formas de representar al mismo número complejo que facilitan las operaciones, éstas son la forma polar y la forma exponencial. 

Cuando hablamos de la forma polar de un número complejo, nos referimos a un segmento de recta que está ubicado en un plano rectangular. Este segmento de recta tiene dos características importantes, tiene un ángulo medido desde el eje horizontal positivo hasta el segmento de recta y además, el segmento de recta tiene una longitud, tal y como se muestra en la siguiente figura:

 La distancia del segmento de recta se calcula igual que el modulo del número complejo expresado en forma rectangular:

 


Mientras que el ángulo lo obtendremos como:

El ángulo de un número complejo no es único. Si medimos el ángulo en sentido contrario a las manecillas del reloj se considera un ángulo positivo, pero si medimos el ángulo en sentido de las manecillas del reloj será un ángulo negativo

1.5 Teorema de De Moivre, potencias y extracción de raíces de un número complejo.

El teorema de De Moivre lo empleamos cuando queremos encontrar las enésimas potencias de un número complejo. Para iniciar el procedimiento de deducción de la fórmula, consideremos a dos números complejos

En el caso en que la ecuación anterior                               resulta:  

                              

Ahora, si tenemos tres números complejos iguales                                 el producto sería:

1.6 Ecuaciones polinómicas.

Ecuaciones polinómicas enteras

Las ecuaciones polinómicas son de la forma P(x) = 0 , donde P(x) es un polinomio.

Grado de una ecuación

El grado de una ecuación es el mayor de los grados de los monomios que forman sus miembros.

Tipos de ecuaciones polinómicas

1. Ecuaciones de primer grado o lineales

Son del tipo ax + b = 0 , con a ≠ 0, ó cualquier otra ecuación en la que al operar, trasponer términos y simplificar adoptan esa expresión.

(x + 1)² = x² - 2

x² + 2x + 1 = x² - 2

2x + 1 = -2

2x + 3 = 0

2. Ecuaciones de segundo grado o cuadráticas

Son ecuaciones del tipo ax² + bx + c = 0, con a ≠ 0.

Ecuaciones de segundo grado incompletas

ax² = 0

ax² + b = 0

ax² + bx = 0

3. Ecuaciones de tercer grado

Son ecuaciones del tipo ax³ + bx² + cx + d = 0, con a ≠ 0.

4. Ecuaciones de cuarto grado

Son ecuaciones del tipo ax⁴ + bx³ + cx² + dx + e = 0, con a ≠ 0.

Ecuaciones bicuadradas

Son ecuaciones de cuarto grado que no tiene términos de grado impar.

ax⁴ + bx² + c = 0, con a ≠ 0.

5. Ecuaciones de grado n

En general, las ecuaciones de grado n son de la forma:

a₁xⁿ + a₂x^n-1 + a₃x^n-2 + ...+ a₀ = 0